Circumference of a Circle

The smallest distance around the circle is called circumference and it can be calculated if the radius is known. The popular equation requires the diameter to be known, which in turn in always double the radius. Therefore the calculation is always an equation with one unknown:

Calculation Background

Solving the mathematical equation is usually the solution to most of the problems faced by the math students. However in the real life other practical methods exist to find the circumference of a circle. Imagine finding yourself in the need of calculating the circumference of a circular ring. Obviously it would be difficult to find the exact radius or diameter of such and object. In this case the simple solution is to make a mark on the ring and place it so that the mark touches the floor. Then we place another mark on the floor in the exact place where we have the mark on the ring. Next it is enough to roll the ring to the point when in makes the full revolution and the mark ends directly on the floor again. We make another mark in that place on the floor. Now we can simply calculate the distance between the two marks on the floor using simple tape measure. This distance will be equal to the circumference of the given ring. Rolling the ring we have to make sure the ring does not slide as this would falsify the result of the measurement.

There are plenty of real life situations when this sort of calculation comes handy. The simple example is how you could figure out how much wrapping paper is needed to wrap some circular object: a bottle, a rolled slipping bag. Or how long of a ribbon you need to put around a football. Understanding the principle of calculating the circumference of a circle is crucial to comprehend how speedometers work, whether it is in a car or in a bicycle. If you are a little bit of a handyman you might in the past mounted a speedometer on your bike. You may remember that it is always necessary to make a basic setup so that the device shows the speed correctly. Usually except from attaching the device to the crossbar it is required to select the size of the bike’s wheel. This size is typically indicated on the tire itself in some sort of standardized notation. This notation obviously carries the huge significance to the digital meter as it will be used to calculate what is the distance the bike covers with one wheel revolution. The sensor on the crossbar detect every full revolution and send in to the meter that additionally keeps time. Knowing the distance that has been covered and the time it took the meter calculates the speed using the simple equation: speed = distance / time. If we take the distance in miles and time in hours we will get the speed in MPH.

An interesting observation is that if the diameter of a circle is equal 1, its circumference is exactly the π value, namely 3.14.

Let’s have a look at several examples of the formula application. The following two simple exercises put the theory in the practical use and hopefully will help to clear any uncertainty that you still may have.

Exercise 1: Calculate the circumference of a circle with a radius of 4 inch.

Solution: Using the standard equation the circumference is calculated in the following manner:

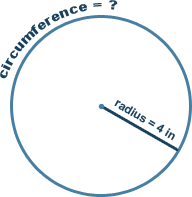Exercise 2: The circumference of a circle equals 10 meters. How long is the diameter of that circle?

Solution: Solving this exercise requires to turn the equation around as the circumference is the known factor while the diameter is the unknown we need to find. As it has been said before the diameter is double the length the radius. Therefore we will use the following two equations to solve the exercise:

Transforming the original equation we calculated that the diameter of the circle with circumference of 10 meters is 3.18 meters. Obviously knowing that we can easily find the radius of that circle as it is exactly a half of its diameter: 1.59 meters.

As you can see from the given examples calculating circumference of a circle is a pretty simple task as it requires only a straightforward multiplication. The only uncertainty may arise with regards to the π value, as not being able to use the exact value we always have to use some sort of its approximation. However in most of the appliances rounding the value to 3.14 is sufficient.